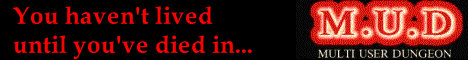I decided to do a "back-of-the-envelope" calculation to see for myself why dark matter can explain, at least qualitatively, the anomalous rotation of galaxies.
The problem: if you move around the center of a galaxy in an approximately circular orbit, the farther you are from the center, the slower you should be moving. Observational evidence contradicts this: the velocities of stars in distant galaxies do not appear to fall off with distance.
Numerically, in the first approximation, if you assume that most of the mass of a galaxy is concentrated in its center, in the outlying regions, the gravitational potential should be proportional to $-1/r$. The kinetic energy of a star orbiting the galactic center should be proportional to this, but kinetic energy is also proportional to $v^2$, where $v$ is the star's velocity. If $v^2\sim 1/r$, then $v\sim 1/\sqrt{r}$, so stellar velocities should be proportional to the inverse square root of radial distance. Actual observations, however, reveal velocity curves that are nearly flat.
One possibility is that the galaxy is surrounded by "dark matter", characterized by the following important properties:
- It interacts with normal matter only gravitationally
- It is not present in substantial quantities in regions dominated by normal matter
Unfortunately, it is not sufficient to simply propose a homogeneous distribution of dark matter with spherical "cavities" in which galaxies are situated. That is because a well known result from classical physics shows that inside such a spherical cavity, the gravitational potential is constant, and there is no net gravitational force (from the surrounding matter), so such a dark matter distribution would not influence galaxy rotation.
To prove this result, we need to compute the gravitational potential at a point $\vec{P}$, by integrating over all points $\vec{R}$ that lie within a spherical shell of inner radius $R_1$, outer radius $R_2$. The integral can be computed without much difficulty if we find a suitable volume element. One such volume element can be obtained by setting up a coordinate system as depicted in Figure 1.
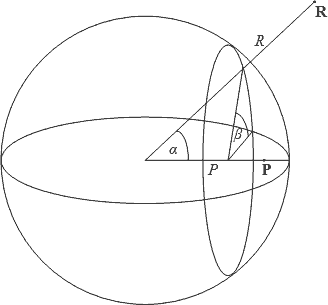
Figure 1: A suitable coordinate system for integrating the volume of a spherical shell.
Using coordinates $R$, $\alpha$ and $\beta$, the distance between points $\vec{P}$ and $\vec{R}$ can be calculated as $r=\sqrt{P^2+R^2-2PR\cos\alpha}$. The volume element at point $\vec{R}$ would be $dV=R^2\sin\alpha~dRd\alpha d\beta$. The gravitational potential at point $\vec{P}$ due to the volume element at point $\vec{R}$ will be proportional to $-1/r$. So all we need to calculate is the integral $\int-1/r~dV$, using integration limits of $\alpha=0...\pi$, $\beta=0...2\pi$ and $R=R_1...R_2$. This definite integral can be computed exactly for the case when $P\gt 0$ and $R\gt P$. The result is $2\pi(R_1^2-R_2^2)$. As the result is not dependent on the value of $P$, it is constant throughout the interior of the cavity. A constant potential means zero gradient, and no net gravitational force.
But this is rather counterproductive, isn't it! This result basically proves that dark matter cannot offer a solution for the galaxy rotation issue. So why do so many clever people insist on the opposite?
To answer that question, consider a different kind of dark matter distribution. Rather than having a cavity with sharp boundary, imagine a dark matter distribution that is smooth, for instance characterized by the function $1-e^{-r^2}$ (Figure 2).
Figure 2: The assumed peculiar distribution of dark matter, as a function of radial distance.
So now the potential function will be $(1-e^{-r^2})/r$, and we need to compute the integral $\int-(1-e^{-r^2})/r~dV$. This integral can also be evaluated, but the result is no longer independent of the value of $P$. On the contrary, when plotted as a function of $P$, the potential would look like that shown in Figure 3.
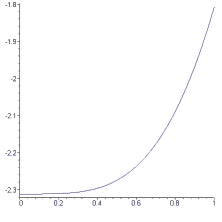
Figure 3: The gravitational potential of the dark matter "halo" shown in Figure 2.
Contrast this curve with the gravitational "potential well" of a point mass, shown in Figure 4.
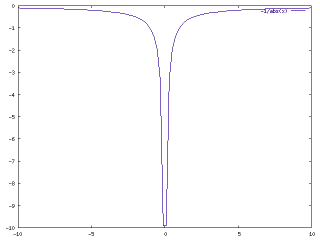
Figure 4: The gravitational potential well of a point mass.
What is remarkable when you compare these two curves is that just when the "potential well" flattens at greater radial distance, the gravitational potential due to the surrounding dark matter becomes steeper. This is precisely what it takes to "flatten out" the rotation curves of a galaxy, causing stars far from the center to move faster than they would if influenced only by the gravitational attraction of the galaxy itself.
Qualitatively this all makes sense, but to verify if these ideas are valid, it is necessary to get some quantitative results. Specifically, one needs to compare the actual mass and rotational curve of a galaxy, and estimate what kind of dark matter distribution it would take to produce that rotational curve.
Taking a visible galactic mass of $4\times 10^{41}~{\rm kg}$ (approximately $2\times 10^{11}$ solar masses), and a galactic radius of $5\times 10^{20}$ meters (roughly 50,000 light-years), and assuming a dark matter "halo" with a characteristic radius of twice the galactic radius and a mass distribution of $1-e^{-r^2}$, as discussed above, I get a gravitational potential that "flattens out" very nicely if the asymptotic value of the halo mass density is on the order of $10^{-20}~{\rm kg}/{\rm m}^3$, as shown in Figure 5.
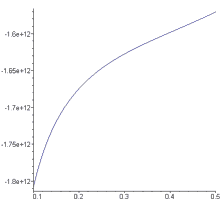
Figure 5: The gravitational potential, as a function of radial distance, around a point mass that is surrounded by a dark matter halo.
This is a very high value compared to the critical density of the universe ($\sim 10^{-26}~{\rm kg}/{\rm m}^3$), but how much mass would it represent? Integrating $1-e^{-r^2}$ over the unit sphere I get 1.81, or about 0.43 times the volume of the unit sphere. For a sphere with a radius of $10^{21}$ meters and a matter density of $10^{-21}~{\rm kg}/{\rm m}^3$, the mass is about $4.2\times 10^{43}~{\rm kg}$, and 0.43 times that amount is about $1.8\times 10^{43}~{\rm kg}$, or about 45 times the (visible) galactic mass.
This is very interesting, because it shows that even a "back of the envelope" calculation can reproduce, well within an order of magnitude, the amount of "missing mass" that dark matter theory predicts.
So if it works out so well, why is dark matter controversial? One very simple reason: Figure 2. What kind of matter would assume this peculiar distribution? What force is responsible for removing dark matter from regions dominated by ordinary matter, even though the two types of matter are gravitationally attracted to each other?
It is these questions that motivate researchers like John Moffat, who are busy developing alternate theories that do not involve dark matter.
Then of course there are also people who believe that the problem doesn't even exist in the first place: that once you take relativity properly into account, the rotation of galaxies turns out to be perfectly normal! I'm not sure, but upon first reading, the paper certainly appeared convincing.