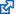There are many excellent books and monographs describing the Standard Model of Particle Physics. One of the best is The Standard Model: A Primer, by Burgess and Moore.
 The Standard Model Lagrangian, that horrendous multiline expression has little meaning without context, and Burgess and Moore is about as concise as they can possibly be, yet the context still fills a book. Instead, here is this diagram from Wikipedia, showing the particle content of the model.
The Standard Model Lagrangian, that horrendous multiline expression has little meaning without context, and Burgess and Moore is about as concise as they can possibly be, yet the context still fills a book. Instead, here is this diagram from Wikipedia, showing the particle content of the model.
However, it is meaningful to recall the dimensionless free parameters of the theory.
In no particular order:
- The so-called fine structure constant, $\alpha$, which determines the coupling strength of electromagnetism or, equivalently, the magnitude of the electron charge;
- The Weinberg angle or weak mixing angle $\theta_W$ that determines the relationship between the coupling constant of electromagnetism and that of the weak interaction;
- The electroweak symmetry breaking energy scale (or the Higgs potential vacuum expectation value, v.e.v.) $v$; alternatively, in place of the $\theta_W$ and $v$, we could have the masses of the $W$ and $Z$ bosons, $m_W$ and $m_Z$;
- The Higgs potential coupling constant $\lambda$ or alternatively, the Higgs mass $m_H$;
- The three mixing angles $\theta_{12}$, $\theta_{23}$, $\theta_{13}$ and the CP-violating phase $\delta_{13}$ of the Cabibbo-Kobayashi-Maskawa (CKM) matrix, which determines how quarks of various flavor can mix when they interact;
- The coupling constant $g_3$ of the strong interaction;
- Nine Yukawa coupling constants that determine the masses of the nine charged fermions (six quarks, three charged leptons).
These are the famous 18 parameters so far of the original Standard Model. It is interesting to note that 15 out of the 18 (the 9 Yukawa fermion mass terms, the Higgs mass, the Higgs potential v.e.v., and the four CKM values) are related to the Higgs boson. In other words, most of our ignorance in the Standard Model is related to the Higgs.
Beyond the 18 parameters, however, there are a few more. First, $\Theta_3$, which would characterize the CP symmetry violation of the strong interaction. Experimentally, $\Theta_3$ is determined to be very small, its value consistent with zero. But why is $\Theta_3$ so small? One possible explanation involves a new hypothetical particle, the axion, which in turn would introduce a new parameter, the mass scale $f_a$ into the theory.
Finally, the canonical form of the Standard Model includes massless neutrinos. We know that neutrinos must have mass, and also that they oscillate (turn into one another), which means that their mass eigenstates do not coincide with their eigenstates with respect to the weak interaction. Thus, another mixing matrix must be involved, which is called the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix. So we end up with three neutrino masses $m_{1}$, $m_2$ and $m_3$, and the three angles $\theta_{12}$, $\theta_{23}$ and $\theta_{13}$(not to be confused with the CKM angles above) plus the CP-violating phase $\delta_{\rm CP}$ of the PMNS matrix.
So this is potentially as many as 26 parameters in the Standard Model that need to be determined by experiment. This is quite a long way away from the “holy grail” of theoretical physics, a theory that combines all four interactions, all the particle content, and which preferably has no free parameters whatsoever. Nonetheless the theory, and the level of our understanding of Nature’s fundamental building blocks that it represents, is a remarkable intellectual achievement of our era.
As to the values of the dimensionless parameters, they can be found on Wikipedia., the NIST CODATA Web site, or at the Web site of the Particle Data Group. As of late 2023, the following values are reported (NB: $m_P$ is the Planck mass):
| Dimensionless parameter | Value |
| $\alpha$ | $7.2973525693(11)\times 10^{-3}$ |
| $\sin^2\theta_W$ | $0.22290(30)$ |
| $v/m_Pc^2$ | $1.9840\times 10^{-17}$ |
| $m_H/m_P$ | $1.0247\times 10^{-17}$ |
| $\theta_{12}$ | $0.22759\pm 8.73\times 10^{-4}$ |
| $\theta_{23}$ | $0.04154\pm 0.00105$ |
| $\theta_{13}$ | $0.003508\pm 1.92\times 10^{-4}$ |
| $\delta_{13}$ | $1.201\pm 0.0785$ |
| $g_3$ | $\sim 1$ |
| $m_e/m_P$ | $4.18546\times 10^{-23}$ |
| $m_\mu/m_P$ | $8.65418\times 10^{-21}$ |
| $m_\tau/m_P$ | $1.45535\times 10^{-19}$ |
| $m_u/m_P$ | $(1.4..2.7)\times 10^{-22}$ |
| $m_d/m_P$ | $(3.4..4.8)\times 10^{-22}$ |
| $m_c/m_P$ | $1.04\times 10^{-19}$ |
| $m_s/m_P$ | $8.27\times 10^{-21}$ |
| $m_t/m_P$ | $1.415\times 10^{-17}$ |
| $m_b/m_P$ | $3.43\times 10^{-19}$ |
| $\Theta_3$ | $\sim 0$ |
| $m_1/m_P$ | $\le 9\times 10^{-30}$ |
| $m_2/m_P$ | $\le 1.6\times 10^{-28}$ |
| $m_3/m_P$ | $\le 1.6\times 10^{-28}$ |
| $\theta_{12}$ (PMNS) | $0.58364\pm 0.0122$ |
| $\theta_{23}$ (PMNS) | $0.8587^{+0.0175}_{-0.0227}$ |
| $\theta_{13}$ (PMNS) | $0.1496^{+0.00227}_{-0.00209}$ |
| $\delta_{\rm CP}$ | $2.95..4.294$ |