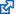This is a simple cosmology calculator. It can be used to compute the age of the universe for a given set of parameters, as well as the comoving distance and light travel time for a given redshift.
| Parameter | Symbol | Value | Unit | |
|---|---|---|---|---|
| Hubble constant | $H_0$ | km/s/Mpc | ||
| Matter density | $\Omega_m$ | |||
| Dark energy density | $\Omega_\Lambda$ | |||
| Radiation density | $\Omega_\gamma$ | |||
| — | Spatial curvature | $\Omega_k$ | ||
| Age of the universe | $t_0$ | Gyr | ||
| Redshift | $z$ | |||
| Age at redshift | $t$ | Gyr | ||
| Light travel time | Gyr | |||
| Comoving distance | $d$ | Mpc | ||
| Transverse comoving distance | $d_T$ | Mpc | ||
| Angular diameter distance | $d_A$ | Mpc | ||
| Luminosity distance | $d_L$ | Mpc | ||
The age of the universe at redshift $z$ is calculated using [1]:
$$t(z)=\frac{1}{H_0}\int_0^{1/(1+z)}\frac{dx}{x\sqrt{\Omega_\Lambda+\Omega_kx^{-2}+\Omega_mx^{-3}+\Omega_\gamma x^{-4}}}.$$
The comoving distance, in turn, is calculated as
$$d(z)=\frac{c}{H_0}\int_0^z\frac{dx}{\sqrt{\Omega_\Lambda+\Omega_k(1+x)^2+\Omega_m(1+x)^3+\Omega_\gamma(1+x)^4}}.$$
The transverse comoving distance is related to the comoving distance by $d_T=\sinh(\sqrt{K}~d)/\sqrt{K}$ where $K=(H_0/c)^2\Omega_k$. When $K=0$, this is just the same as the comoving distance. (The expression is real-valued even when $K<0$; in that case, an equivalent form using the ordinary sine function and $-K$ can also be used.)
The angular diameter distance and luminosity distance are given by $d_A=d_T/(1+z)$ and $d_L=d_T(1+z)$, respectively.
Results may differ from those calculated using other cosmology calculators because of different rounding (in numerical integration, in particular) and, well, because this one is brand spanking new and may have bugs!
[1] Weinberg, S: Cosmology, Oxford U. Press (2008)